미분방정식 완벽 정복! 초보자부터 전문가까지, 당신의 수학 고민 해결사
작성자 정보
- 미분방정식 작성
- 작성일
컨텐츠 정보
- 176 조회
- 목록
본문
이 게시물에는 경제적 보상이 포함된 제휴 링크가 있습니다.
미분방정식 때문에 고민이신가요? 어려운 개념, 복잡한 문제 풀이에 막막함을 느끼시나요? 더 이상 걱정하지 마세요! 본 가이드는 미분방정식의 기초부터 심화 내용까지, 초보자도 쉽게 이해하고, 전문가도 활용할 수 있는 풍부한 정보를 제공합니다. 이제 미분방정식의 세계를 흥미롭고 효율적으로 탐험해 보세요!
미분방정식 필수정보 미리보기
- 미분방정식의 정의와 종류
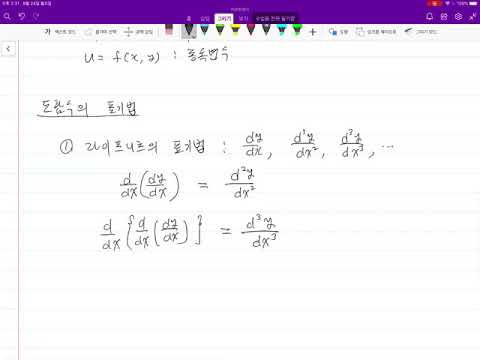
- 미분방정식 풀이 방법: 다양한 기법 소개 (변수분리, 적분인자, 라플라스 변환 등)
- 실제 예시와 문제 풀이 과정 상세 설명
- 미분방정식 활용 분야: 공학, 물리, 경제 등 다양한 분야에서의 응용 사례
- 효과적인 학습 전략 및 추천 학습 자료
미분방정식이란 무엇일까요? 쉽게 이해하는 미분방정식 개념
미분방정식은 말 그대로 미분을 포함하는 방정식입니다. 쉽게 말해, 어떤 함수와 그 함수의 도함수(미분) 사이의 관계를 나타내는 수학적 표현이죠. 예를 들어, 물체의 속도가 시간에 따라 변하는 것을 설명하는 방정식이 바로 미분방정식입니다. 속도는 위치의 변화율(미분)이기 때문이죠. 우리가 주변에서 접하는 많은 현상들이 미분방정식으로 표현될 수 있다는 사실, 놀랍지 않나요? 이처럼 미분방정식은 자연 현상을 수학적으로 모델링하고 분석하는 강력한 도구입니다.
어떤 종류의 미분방정식이 있을까요? 다양한 미분방정식의 세계
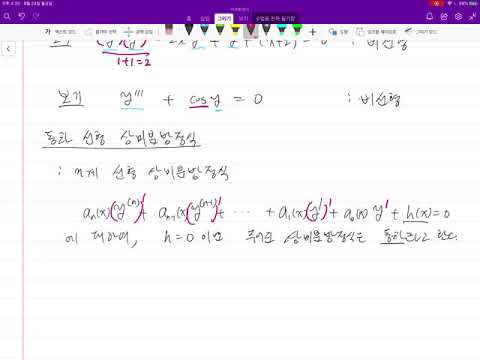
미분방정식은 크게 상미분방정식과 편미분방정식으로 나뉩니다. 상미분방정식은 하나의 독립 변수만 포함하는 반면, 편미분방정식은 두 개 이상의 독립 변수를 포함합니다. 또한, 선형 미분방정식과 비선형 미분방정식, 그리고 그 차수에 따라서도 다양하게 분류됩니다.
| 미분방정식 종류 | 설명 | 예시 |
|---|---|---|
| 상미분방정식 (Ordinary Differential Equation, ODE) | 하나의 독립 변수를 갖는 미분방정식 | dy/dx + y = x |
| 편미분방정식 (Partial Differential Equation, PDE) | 두 개 이상의 독립 변수를 갖는 미분방정식 | ∂²u/∂x² + ∂²u/∂y² = 0 (Laplace 방정식) |
| 선형 미분방정식 | 미지함수와 그 도함수가 선형적으로 나타나는 미분방정식 | ay'' + by' + cy = 0 |
| 비선형 미분방정식 | 미지함수 또는 그 도함수가 비선형적으로 나타나는 미분방정식 | y' = y² + x |
| 1차 미분방정식 | 최고차 미분의 차수가 1인 미분방정식 | dy/dx + 2y = x² |
| 2차 미분방정식 | 최고차 미분의 차수가 2인 미분방정식 | y'' + 3y' + 2y = sin(x) |
미분방정식, 어떻게 풀까요? 다양한 풀이 기법 소개
미분방정식을 푸는 방법은 다양합니다. 변수분리법, 적분인자법, 라플라스 변환 등 여러 가지 기법이 있으며, 문제의 특성에 따라 적절한 방법을 선택해야 합니다. 각 기법은 장단점이 있으므로, 다양한 기법을 익혀두는 것이 좋습니다. 본 가이드에서는 각 기법에 대한 상세한 설명과 예제를 제공하여 여러분의 이해를 돕습니다.
미분방정식은 어디에 사용될까요? 다양한 응용 분야
미분방정식은 공학, 물리학, 생물학, 경제학 등 다양한 분야에서 널리 활용됩니다. 예를 들어, 전기 회로의 해석, 열전달 현상의 모델링, 인구 변화 예측 등에 미분방정식이 사용됩니다. 본 가이드에서는 각 분야에서 미분방정식이 어떻게 활용되는지 다양한 예시를 통해 보여드립니다.
미분방정식 학습, 효과적으로 하는 방법은?
미분방정식 학습은 연습과 꾸준함이 중요합니다. 다양한 문제를 풀어보면서 개념을 익히고, 어려운 문제는 여러 번 반복해서 풀어보는 것이 좋습니다. 또한, 온라인 강의나 학습 자료를 활용하여 이해가 부족한 부분을 보충할 수 있습니다. 본 가이드는 효과적인 학습 전략과 추천 학습 자료를 제공하여 여러분의 학습을 지원합니다.
본 가이드의 핵심 가치: 최고의 학습 경험 제공
본 가이드는 다음과 같은 핵심 가치를 제공합니다.
- 명확하고 체계적인 설명: 복잡한 개념을 쉽고 명확하게 설명하여 누구나 쉽게 이해할 수 있도록 합니다.
- 다양한 예제와 문제: 풍부한 예제와 문제를 통해 실제로 미분방정식을 활용하는 방법을 익힐 수 있도록 합니다.
- 실용적인 학습 전략: 효과적인 학습 전략과 추천 학습 자료를 제공하여 학습 효율을 높입니다.
- 합리적인 가격: 최고의 품질을 합리적인 가격으로 제공합니다. (가격 정보는 별도 문의)
결론적으로, 본 가이드는 미분방정식 학습에 필요한 모든 것을 담고 있습니다. 이제 미분방정식에 대한 두려움을 버리고, 본 가이드와 함께 미분방정식의 세계를 즐겁게 탐험해 보세요! 여러분의 수학적 성장을 응원합니다!
상품상세보기 : 미분방정식 상품 비교, 할인정보 바로가기
네이버백과 검색 네이버사전 검색 위키백과 검색
미분방정식 관련 동영상








미분방정식 관련 상품검색
관련자료
-
이전
-
다음


